当 我们与大语言模型(LLMs)对话时,会感觉这些模型是可以理解语句其中的含义的。但事实上,该系统是依靠数字、向量和数学来寻找单词和句子之间的关系来运作的。
实现这项功能的最重要工具之一是余弦相似度。想要知道 LLMs 如何判断两个句子意思的相似性,余弦相似度则是其中的关键。
本文将用通俗易懂的语言来解释了余弦相似度,展示其背后的数学原理,并将其与现代语言模型的工作原理联系起来。最终,我们将明白为什么这个测量向量之间角度的简单方法就能够驱动搜索、聊天机器人以及许多其他人工智能系统。
1] 余弦相似度简介
假设现在有两个句子,这对计算机来说,它们不是单词,而是向量,一长串用来表达含义的数字。
余弦相似度衡量的是这两个向量的接近程度,不是通过它们的长度,而是通过它们之间的角度。
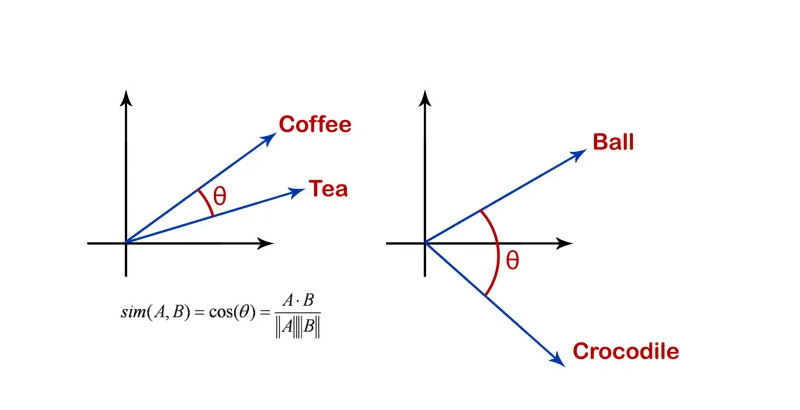
图.1 余弦相似度示意图
想象一下,从同一点出发的两支箭头。如果它们指向同一方向,则它们之间的角度为零,余弦相似度为1;如果它们指向相反的方向,则角度为180度,余弦相似度为-1;如果它们成直角,则余弦相似度为零。
因此,余弦相似度告诉我们两个向量是否指向相同的方向。在语言任务中,这意味着两段文本是否具有相似的含义。
2] 余弦相似度数学原理
要理解余弦相似度,我们需要了解一些数学知识。几何中,角的余弦是两个向量的点积与它们幅值的乘积之比。余弦相似度的公式如下:
cosine_similarity(A, B) = (A · B) / (||A|| * ||B||)
公式中:
- A · B 是向量 A 和 B 的点积
- ||A|| 是向量 A 的模(长度)
- ||B|| 是向量 B 的模
点积是将两个向量中对应的数字相乘,然后相加。向量的模值就像用勾股定理求箭头的长度一样。
该公式始终给出介于 -1 和 1 之间的值。接近 1 的值表示两个向量几乎指向同一方向。接近 0 的值表示它们不相关。接近 -1 的值表示它们方向相反。
3] 简单示例
让我们看一个使用 Python 语言编写的简短示例。假设我们想要检查两段短文本的相似度。就可以使用 scikit-learn 将它们转换为向量,然后计算其余弦相似度。
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import cosine_similarity
texts = [
"I love machine learning",
"I love deep learning"
]
vectorizer = TfidfVectorizer().fit_transform(texts)
vectors = vectorizer.toarray()
similarity = cosine_similarity([vectors[0]], [vectors[1]])
print("Cosine similarity:", similarity[0][0])
代码首先导入了两个重要的工具:TfidfVectorizer 负责将文本转换为数字,而 cosine_similarity 则用于测量两组数字的相似度。它们共同作用,就可以让我们能够以计算机可以理解的方式比较文本相似性。
接下来,我们定义要比较的句子。在本例中,我们使用”I love machine learning”和”I love deep learning”。这两个句子有一些共同的词,例如”I”、”love”和”learning”,但有一个词不同:”machine”和”deep”。这使得它们成为很好的测试样本,因为它们显然相关,但并不完全相同。
然后,向量化器会根据这两个句子中所有不重复的词构建一个词汇表。对于这些输入,词汇表变为 [“deep”, “learning”, “love”, “machine”]。这意味着程序现在拥有了一个列表,其中包含了在构建句子的数值表示时将要跟踪的所有词。
之后,每个句子都会被转换成一个向量,它只是一个数字列表。这些数字不仅仅是原始的词数。相反,它们使用 TF-IDF(词频-逆文档频率)进行加权。
TF-IDF 会提高句子中重要词汇的重要性,而降低非常常见的词汇的重要性。简化后,第一个句子会变成[0. 0.50154891 0.50154891 0.70490949],而第二个句子会变成[0.70490949 0.50154891 0.50154891 0. ]。这些数字可能看起来很小,但重要的是它们的相对值。
然后,使用 .toarray() 方法将这些向量转换为标准 Python 数组。这使得它们更易于处理,因为 TF-IDF 输出默认以特殊的稀疏格式存储。
将句子表示为向量后,就可以应用余弦相似度。此步骤可以检查两个向量之间的角度。
如果两个向量指向完全相同的方向,它们的相似度得分为 1。如果它们不相关,得分接近于 0。如果它们指向相反的方向,得分为负。
在本例中,由于两个句子大部分词汇相同,向量指向相似方向,因此余弦相似度在 0.5 到 0.7 之间。
简而言之,这段代码展示了计算机如何通过将两个句子转换为数字向量,然后检查这些向量的相似程度来比较它们。通过使用余弦相似度,程序不仅可以判断句子是否共享词汇,还可以判断它们在语义上的重叠程度。
4] 嵌入式余弦相似度
在实践中,像 GPT 或 BERT 这样的 LLM 并不使用简单的字数统计,而是使用嵌入向量。
嵌入向量是一个用于捕捉含义的密集向量。每个单词、短语或句子都会被转换成一组数字,并将其置于高维空间中。
在这个空间,含义相近的单词彼此靠近。例如,”国王”和”女王”的嵌入向量比”国王”和”桌子”的嵌入向量更接近。
余弦相似度是一种工具,可以让我们衡量两个嵌入向量的接近程度。例如当要搜索”狗”时,系统就可以查找指向相似方向的嵌入向量。这样,即使查询中没有包含这些确切的词,系统也会找到关于”小狗”、”犬科动物”或”宠物”这样的结果。
5] LLM 如何使用余弦相似度
大型语言模型以多种方式使用余弦相似度。当我们提出问题时,模型会将输入内容编码为一个向量。然后,它会使用余弦相似度将此向量与存储的知识或候选答案进行比较。
对于语义搜索,余弦相似度有助于对文档进行排序。系统可以将所有文档嵌入到向量中,然后嵌入我们的查询并计算相似度得分,得分最高的文档最相关。
在聚类中,余弦相似度有助于将具有相关含义的句子分组。在推荐系统中,它通过比较用户的偏好向量来帮助将用户与项目匹配。
即使在生成答案时,LLM 也依赖向量相似度来确定哪些单词或短语在上下文中表现最佳。余弦相似度为模型提供了一种简单而强大的方法来衡量含义的接近度。
6] 余弦相似度的局限性
虽然余弦相似度非常强大,但它也有局限性。它很大程度上取决于嵌入的质量。如果嵌入不能很好地捕捉含义,相似度得分可能无法反映现实世界的相似度。
此外,余弦相似度仅衡量方向。有时,幅度也包含有用的信息。例如,句子嵌入的长度可能反映置信度。忽略它,余弦相似度可能会丢失部分信息。
尽管存在这些局限性,余弦相似度仍然是自然语言处理中最广泛使用的方法之一。
7] 余弦相似度对于 LLM 的重要性
余弦相似度不仅仅是一个数学技巧,它还是人类语言与机器理解之间的桥梁。它允许模型将意义视为几何图形,将问题和答案转化为空间中的点。
如果没有余弦相似度,嵌入的实用性就会降低,语义搜索、聚类和排名等任务也会变得更加困难。通过将问题简化为角度测量,我们使意义变得可测量且可用。
每当我们上网搜索、与 AI 聊天或使用推荐引擎时,余弦相似度都在幕后发挥作用。
余弦相似度解释了 LLM 如何判断单词、句子甚至整篇文档之间含义的接近程度。它的工作原理是比较向量之间的角度,而不是向量的长度,这使得它非常适合文本分析。借助嵌入,余弦相似度成为语义搜索、聚类、推荐以及许多其他自然语言处理任务的基础。
下次遇到当人工智能(AI)给出一个让人感觉”足够接近”的答案时,要知道,一个简单的数学概念——测量两个箭头之间的角度——正在完成大部分繁重的工作。